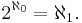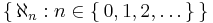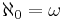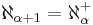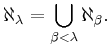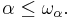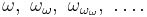Aleph number
In set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality (or size) of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph (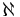 ).
).
The cardinality of the natural numbers is 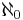 (read aleph-naught, aleph-null or aleph-zero), the next larger cardinality is aleph-one
(read aleph-naught, aleph-null or aleph-zero), the next larger cardinality is aleph-one 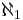 , then
, then 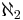 and so on. Continuing in this manner, it is possible to define a cardinal number
and so on. Continuing in this manner, it is possible to define a cardinal number 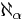 for every ordinal number α, as described below.
for every ordinal number α, as described below.
The concept goes back to Georg Cantor, who defined the notion of cardinality and realized that infinite sets can have different cardinalities.
The aleph numbers differ from the infinity (∞) commonly found in algebra and calculus. Alephs measure the sizes of sets; infinity, on the other hand, is commonly defined as an extreme limit of the real number line (applied to a function or sequence that "diverges to infinity" or "increases without bound"), or an extreme point of the extended real number line.
Contents |
Aleph-naught
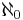 is the cardinality of the set of all natural numbers, and is the first transfinite cardinal. A set has cardinality
is the cardinality of the set of all natural numbers, and is the first transfinite cardinal. A set has cardinality 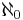 if and only if it is countably infinite, which is the case if and only if it can be put into a direct bijection, or "one-to-one correspondence", with the natural numbers. Such sets include the set of all prime numbers, the set of all integers, the set of all rational numbers, the set of algebraic numbers, the set of binary strings of all finite lengths, and the set of all finite subsets of any countably infinite set.
if and only if it is countably infinite, which is the case if and only if it can be put into a direct bijection, or "one-to-one correspondence", with the natural numbers. Such sets include the set of all prime numbers, the set of all integers, the set of all rational numbers, the set of algebraic numbers, the set of binary strings of all finite lengths, and the set of all finite subsets of any countably infinite set.
If the axiom of countable choice (a weaker version of the axiom of choice) holds, then 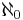 is smaller than any other infinite cardinal.
is smaller than any other infinite cardinal.
Aleph-one
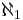 is the cardinality of the set of all countable ordinal numbers, called ω1 or (sometimes) Ω. Note that this ω1 is itself an ordinal number larger than all countable ones, so it is an uncountable set. Therefore
is the cardinality of the set of all countable ordinal numbers, called ω1 or (sometimes) Ω. Note that this ω1 is itself an ordinal number larger than all countable ones, so it is an uncountable set. Therefore 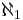 is distinct from
is distinct from 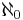 . The definition of
. The definition of 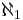 implies (in ZF, Zermelo–Fraenkel set theory without the axiom of choice) that no cardinal number is between
implies (in ZF, Zermelo–Fraenkel set theory without the axiom of choice) that no cardinal number is between 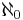 and
and 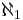 . If the axiom of choice (AC) is used, it can be further proved that the class of cardinal numbers is totally ordered, and thus
. If the axiom of choice (AC) is used, it can be further proved that the class of cardinal numbers is totally ordered, and thus 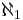 is the second-smallest infinite cardinal number. Using AC we can show one of the most useful properties of the set ω1: any countable subset of ω1 has an upper bound in ω1. (This follows from the fact that a countable union of countable sets is countable, one of the most common applications of AC.) This fact is analogous to the situation in
is the second-smallest infinite cardinal number. Using AC we can show one of the most useful properties of the set ω1: any countable subset of ω1 has an upper bound in ω1. (This follows from the fact that a countable union of countable sets is countable, one of the most common applications of AC.) This fact is analogous to the situation in 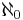 : every finite set of natural numbers has a maximum which is also a natural number; that is, finite unions of finite sets are finite.
: every finite set of natural numbers has a maximum which is also a natural number; that is, finite unions of finite sets are finite.
ω1 is actually a useful concept, if somewhat exotic-sounding. An example application is "closing" with respect to countable operations; e.g., trying to explicitly describe the σ-algebra generated by an arbitrary collection of subsets. This is harder than most explicit descriptions of "generation" in algebra (vector spaces, groups, etc.) because in those cases we only have to close with respect to finite operations—sums, products, and the like. The process involves defining, for each countable ordinal, via transfinite induction, a set by "throwing in" all possible countable unions and complements, and taking the union of all that over all of ω1.
The continuum hypothesis
The cardinality of the set of real numbers (cardinality of the continuum) is 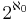 . It is not clear where this number fits in the aleph number hierarchy. It follows from ZFC (Zermelo–Fraenkel set theory with the axiom of choice) that the celebrated continuum hypothesis, CH, is equivalent to the identity
. It is not clear where this number fits in the aleph number hierarchy. It follows from ZFC (Zermelo–Fraenkel set theory with the axiom of choice) that the celebrated continuum hypothesis, CH, is equivalent to the identity
CH is independent of ZFC: it can be neither proven nor disproven within the context of that axiom system (provided that ZFC is consistent). That it is consistent with ZFC was demonstrated by Kurt Gödel in 1940 when he showed that its negation is not a theorem of ZFC. That it is independent of ZFC was demonstrated by Paul Cohen in 1963 when he showed, conversely, that the CH itself is not a theorem of ZFC by the (then novel) method of forcing.
Aleph-ω
Conventionally the smallest infinite ordinal is denoted ω, and the cardinal number 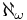 is the least upper bound of
is the least upper bound of
among alephs.
Aleph-ω is the first uncountable cardinal number that can be demonstrated within Zermelo–Fraenkel set theory not to be equal to the cardinality of the set of all real numbers; for any positive integer n we can consistently assume that 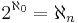 , and moreover it is possible to assume
, and moreover it is possible to assume 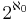 is as large as we like. We are only forced to avoid setting it to certain special cardinals with cofinality
is as large as we like. We are only forced to avoid setting it to certain special cardinals with cofinality 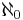 , meaning there is an unbounded function from
, meaning there is an unbounded function from 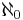 to it.
to it.
Aleph-α for general α
To define 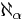 for arbitrary ordinal number
for arbitrary ordinal number  , we must define the successor cardinal operation, which assigns to any cardinal number ρ the next larger well-ordered cardinal ρ+. (If the axiom of choice holds, this is the next larger cardinal.)
, we must define the successor cardinal operation, which assigns to any cardinal number ρ the next larger well-ordered cardinal ρ+. (If the axiom of choice holds, this is the next larger cardinal.)
We can then define the aleph numbers as follows
and for λ, an infinite limit ordinal,
The α-th infinite initial ordinal is written  . Its cardinality is written
. Its cardinality is written 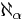 . See initial ordinal.
. See initial ordinal.
In ZFC the 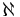 function is a bijection between the ordinals and the infinite cardinals.[1]
function is a bijection between the ordinals and the infinite cardinals.[1]
Fixed points of omega
For any ordinal α we have
In many cases 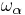 is strictly greater than α. For example, for any successor ordinal α this holds. There are, however, some limit ordinals which are fixed points of the omega function, because of the fixed-point lemma for normal functions. The first such is the limit of the sequence
is strictly greater than α. For example, for any successor ordinal α this holds. There are, however, some limit ordinals which are fixed points of the omega function, because of the fixed-point lemma for normal functions. The first such is the limit of the sequence
Any weakly inaccessible cardinal is also a fixed point of the aleph function.
References
- Notes
- ^ aleph numbers at PlanetMath.
External links
- Weisstein, Eric W., "Aleph-0" from MathWorld.